해당 내용 노션 페이지 : https://skier-song9.notion.site/50276054fa9e44519752a972388cea74?pvs=4
(tistory에서 수식 편집하기 불편해서 수식은 노션 참고... 마크다운이랑 기본모드 왔다 갔다 하면 글자색이랑 이미지 자꾸 제멋대로...)
🔻행렬이란?
🔸구성
- 수나 식을 사각형 모양으로 배열하고 괄호로 묶어 놓은 것

- 성분 (원소, element, entry)
- 피벗 Pivot (추축성분, pivot entry) : 각 행에서 0이 아니고 맨 왼쪽에 위치한 성분
- ex)

- 주대각 성분 (main diagonal entry) : 행과 열의 번호가 같은 성분

- ex) $a_{11},a_{22},a_{33},...$
- 행 (row), 열 (column)
- 크기 (size) : row X columns >> (row by col이라고 읽음)
- 크기가 m by n인 행렬 A를 $A_{m\times n}$으로 표기한다.
- 행벡터, 열벡터

- m by 1 행렬이라 부르기도 하고, 열벡터라 부르기도 한다.1 by n 행렬이라 부르기도 하고, 열벡터라 부르기도 한다.

🔸행렬의 종류
- 전치행렬 Transposed matrix
- 행렬의 행과 열을 각각 치환한 행렬
- 표현 : $\text{행렬}A \text{ 의 }~~ \text{전치행렬은}~A^T$
- 정방행렬(정사각행렬) Square matrix
- 행과 열의 크기가 같은 행렬

- 대각행렬 Diagonal matrix
- 대각선 상의 성분(주대각 성분)을 제외한 모든 성분이 0인 행렬
- 꼭 정방행렬일 필요는 없다.
- $\begin{bmatrix}1 & 0 & 0 \\ 0 & 2 & 0 \\ end{bmatrix} ~~,~~ \begin{bmatrix}1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}$
- 첨가행렬(확대행렬) Augmented matrix
- 행렬방정식에서 계수행렬과 상수벡터를 묶어서 표현한 행렬
- ex) 연립선형방정식을 행렬방정식으로, 행렬방정식을 첨가행렬로 변환한 예시
- $\text{연립선형방정식}~\begin{cases}x_1+2x_2+x_3=3 \\ x_2-x_3=-2 \\ 3x_1-2x_2-3x_3=-1 \end{cases}
$
- $\text{연립선형방정식}~\begin{cases}x_1+2x_2+x_3=3 \\ x_2-x_3=-2 \\ 3x_1-2x_2-3x_3=-1 \end{cases}

- 행 사다리꼴 행렬 Row Echelon Form matrix
- 다음 조건을 만족하는 행렬이다.
- 모든 성분이 0인 행은 맨 아래 행에 있어야 한다.
- 모든 행의 피봇(추축성분)은 위쪽 행의 피봇보다 오른쪽 열에 있다.
- 모든 피봇은 1이고, 피봇 아래쪽의 모든 성분은 0이다.
- 행 사다리꼴 행렬이 아닌 예시)
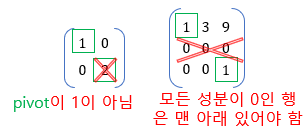
- 행 사다리꼴 행렬인 예시)
- 특징 : 모든 행렬은 ERO(행렬방정식 기본연산 >> 다음 포스트에 등장)를 통해 행 사다리꼴 행렬로 만들 수 있다.
- 다음 조건을 만족하는 행렬이다.
- 기약행 사다리꼴 행렬 Reduced Row Echelon Form matrix
- 모든 피봇이 해당 열에서 0이 아닌 유일한 성분인 행 사다리꼴 행렬이다.
- 즉, 피봇이 있는 열에는 피봇을 제외한 나머지 성분은 모두 0이어야 한다.
- 기약행 사다리꼴 행렬인 예시)

- 기약행 사다리꼴 행렬이 아닌 예시)

- 모든 피봇이 해당 열에서 0이 아닌 유일한 성분인 행 사다리꼴 행렬이다.
- 항등행렬(단위행렬) Identity matrix (unit matrix)
- 주대각 성분이 모두 1이고, 나머지 성분이 모두 0인 행렬
- 대각행렬이면서, 기약행 사다리꼴 행렬인 행렬이다.
- 정방행렬이어야 한다.
- $ \begin{bmatrix}1 & 0\\ 0 & 1\\ \end{bmatrix}~~,~~\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $
- 표기 : $I_n$으로 표기. 정방행렬이므로 n x n 은 표시 안 함.
- 단위행렬은 행렬곱 연산의 항등원이다.
- $ A_{m\times n} \cdot I_n = A_{m\times n} \\I_n\cdot A_{m\times n} = A_{m\times n} $
- 주대각 성분이 모두 1이고, 나머지 성분이 모두 0인 행렬
- 영행렬 Zero matrix
- 모든 성분이 0인 행렬
- 표기 : $\bold{0}{m\times n}$ 또는 ${O}{m \times n}$ . 숫자 0 또는 알파벳 O로 표기

- 행렬 덧셈 연산의 항등원이다.
- $ A_{m\times n} + \bold{0}_{m\times n} = A_{m\times n} \\\bold{O}_{m\times n} + A_{m\times n} = A_{m\times n} $
- 대칭행렬 Symmetric matrix
- 어떤 행렬의 전치행렬이 자기 자신과 같은 행렬
-

- 역행렬 Inverse matrix (역행렬에 대해선 뒤에 연립선형방정식과 행렬방정식 풀이에서 더 자세히 알아볼 예정)
- 역원이란? 연산의 결과가 항등원이 되도록 하는 것
- 정의 : 정방행렬 A에 대해 다음 성질을 만족하는 행렬 B이다.
- $ A=[a_{ij}]_{n\times n}~일~때, \\ AB=BA=I_n인~B가~A의~역원이다.\\ A^{-1}=B $
- 역행렬의 존재여부에 따른 명칭 구분
- 가역행렬, 비특이행렬, 정칙행렬 - invertible , nonsigular , regular matrix : 역행렬이 존재하는 행렬
- 비가역행렬, 특이행렬 - noninvertible , singular matrix : 역행렬이 존재하지 않는 행렬
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 주요 행렬 - 역행렬(1/2) (0) | 2023.09.28 |
|---|---|
| [선형대수] 왜 행렬을 사용하는가?(2/2) - 행렬방정식 (0) | 2023.09.28 |
| [선형대수] 왜 행렬을 사용하는가?(1/2) - 연립선형방정식 (0) | 2023.09.28 |
| [선형대수] 행렬의 연산(합, 곱)과 성질 (2) | 2023.09.26 |
| [선형대수] 시작하기에 앞서, 기초 개념 정리(기호, 진리, 집합, 사상) (0) | 2023.09.25 |

